Visualizing the CAP Theorem in 3D: Navigating the Complexities of Distributed Systems
The CAP theorem, formulated by Eric Brewer, is a fundamental concept in distributed systems. It posits that it's impossible for a distributed data store to simultaneously provide more than two out of the following three guarantees: Consistency, Availability, and Partition tolerance (CAP).
While the CAP theorem provides a foundational framework for understanding distributed systems, its binary representation sometimes oversimplifies the complex reality of these systems.
A more nuanced way to visualize the trade-offs in distributed systems design is to imagine the CAP properties in a three-dimensional space.
Presenting : CAP Theorem as a Cube
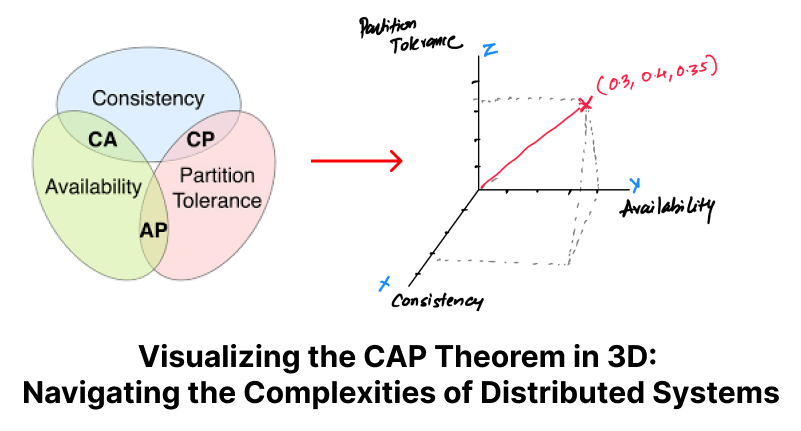
Imagine a cube where each axis (length, width, and height) represents one of the CAP properties - Consistency, Availability, and Partition tolerance. Any point inside this cube represents a particular balance of these three properties.

In this model, a system that perfectly guarantees consistency, availability, and partition tolerance would be at one of the corners of the cube. In reality, such a system doesn't exist due to the trade-offs outlined by the CAP theorem.
Most real-world systems would be represented as points somewhere within the cube, not reaching the ideal state (the corners).
Functional Form : CAP Theorem in 3-Dimension Space
To express this in a functional form in 3D Space, these are the two conditions
- C+A +P < 3
- (CA, CP, AP) < 2
This set of functions and conditions mathematically represents the CAP theorem, stating that it's impossible to maximize all three properties simultaneously in a distributed system, and even the sum of any two properties can't reach 2.
Given the complex nature of distributed systems, it's unfeasible for any such system to perfectly align with a specific point on a 2D plane representing the CAP theorem.
For instance, if a system is fully optimized for Consistency and Availability but not at all for Partition tolerance, its coordinate might be (1, 1, 0) in the 3D CAP space. However, in practice, it's almost impossible for a real-world distributed system to have a zero value for Partition tolerance, because network partitions are a reality that any distributed system must deal with. Therefore, the system would likely have a small but non-zero value for P, placing it somewhere inside the 3D CAP space rather than on the 2D plane.

The Fluid Nature of Real-world Systems
In reality, distributed systems can move within this 3D CAP space based on their design and operational conditions. For instance, a system might normally operate close to the Consistency axis, but during a network partition, it might shift towards the Availability axis to maintain operations.
This 3D visualization of the CAP theorem offers a more nuanced view than the binary CA, AP, CP categories. It serves as a reminder that distributed system design involves a complex interplay of trade-offs, and that the right balance depends on the specific requirements of each use case.
